You have probably heard the claim that ![]() is
an irrational number. That means that
is
an irrational number. That means that ![]() cannot
be expressed as a quotient of two integers. How many other irrational
numbers can you think of? While you may be able to come up with a
few other examples, it is much easier for us to think of examples of rational
numbers! Which kind of number is more plentiful? In this vignette,
we will see not only why
cannot
be expressed as a quotient of two integers. How many other irrational
numbers can you think of? While you may be able to come up with a
few other examples, it is much easier for us to think of examples of rational
numbers! Which kind of number is more plentiful? In this vignette,
we will see not only why ![]() is
irrational, but we will also see evidence that the irrational numbers are
far more plentiful than rationals!
is
irrational, but we will also see evidence that the irrational numbers are
far more plentiful than rationals!
![]() is
Irrational
is
Irrational
To see that ![]() must
be irrational, we will use the method of proof by contradiction introduced
in the vignette on prime numbers. Suppose
that
must
be irrational, we will use the method of proof by contradiction introduced
in the vignette on prime numbers. Suppose
that ![]() were
a rational number. Recalling that
were
a rational number. Recalling that ![]() refers only to the positive square root of 2, this means that
refers only to the positive square root of 2, this means that ![]() could be written as the quotient of two positive integers, say
could be written as the quotient of two positive integers, say ![]() ,
where the fraction is in lowest terms -- that is, a and b
have no common factors. Then simple algebra gives us the following:
,
where the fraction is in lowest terms -- that is, a and b
have no common factors. Then simple algebra gives us the following:
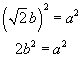
How Many Irrational Numbers are There?
The argument above is not unique to the number 2, and actually applies
to any prime number. Thus, if p is a prime number, then ![]() is an irrational number. Since there are infinitely many primes (as
seen in an earlier vignette), it follows that there are infinitely many
irrational numbers.
is an irrational number. Since there are infinitely many primes (as
seen in an earlier vignette), it follows that there are infinitely many
irrational numbers.
Now in the vignette titled How Big is Infinity?, we saw that the set of rational numbers is countably infinite. Could it be that the set of irrational numbers is also countably infinite? (Pay attention now, because this is tricky -- but really cool!) We also saw that the set of numbers in [0, 1] is uncountable, and of course it follows that the (larger) set of all real numbers must be uncountable as well. But the set of all real numbers is simply the union of the set of rational numbers with the set of irrational numbers. So if the set of irrational numbers were countable, then we would have a union of two countable sets producing an uncountable set. We will now see that this is impossible.
Suppose we have two sets A and B, both of which are countable.
To see that the set ![]() is
also countable, it suffices to exhibit a one-to-one correspondence between
the set of positive integers and the set
is
also countable, it suffices to exhibit a one-to-one correspondence between
the set of positive integers and the set ![]() .
Since
.
Since ![]() and
and ![]() are
countable, we have such one-to-one correspondences for these sets, say
are
countable, we have such one-to-one correspondences for these sets, say
Consequently, if the set of irrational numbers were countable, we would have an argument that the set of real numbers is countable -- since the set of real numbers would then be a union of two countable sets. But we know that the set of real numbers is uncountable. Thus, the set of irrational numbers is uncountable.
Where ARE All of Those Irrationals?
OK, we now know that there are uncountably many irrational numbers. That means that there are far more irrationals than rationals. But we are in the uncomfortable position of not knowing so many of them! Well, we are pretty comfortable with our understanding of rational numbers as fractions -- that is, as quotients of integers. Using decimal representation of numbers, the rational numbers are precisely those whose decimal representation includes a repeating block of digits at the end. (We are counting the terminating decimals as having a repeating 0 at the end.) The irrational numbers, then, are those whose decimal representations do not terminate or repeat. Some examples include the famous numbers
![]()
The rational numbers and the irrationals are interwoven on the number
line, so that between any two rationals (no matter how close they are)
there is an irrational, and between any two irrationals (no matter how
close they are) there is a rational. Thus, there are never any blocks
of "consecutive" rationals or irrationals. As an example, between
the rational numbers ![]() and
and ![]() , we
can find the irrational number
, we
can find the irrational number ![]() .
And between the irrational numbers 7.4367110893... and 7.4367110894...
we can find the rational number
.
And between the irrational numbers 7.4367110893... and 7.4367110894...
we can find the rational number ![]() .
.
Further Exploration