The symbol 
is
usually used in mathematics as a part of other symbols, as an indication
of something that may be arbitrarily large. For example, the customary
interval notation 
refers
to the set of all real numbers greater than or equal to the number a.
That is, is
the set of numbers starting at a, and moving arbitrarily far to
the right. Although we read the symbol ""
by saying "infinity," we must be careful not to think of as
a number.
Countably Infinite Sets
On the other hand, mathematicians frequently use the word "infinite"
as an adjective, when describing the size, or "cardinality," of
a set. Two sets A and B are said to have the same
cardinality if there is a one-to-one correspondence between them.
For example, the sets 
and 
have
the same cardinality, since there is a very obvious one-to-one correspondence
between them. A set A is called countably infinite
if it has the same cardinality as the set 
of
positive integers, 
.
That is, a set is countably infinite if it is possible to devise a systematic
way of pointing to each of its elements in turn, and counting them:
one, two, three, ... .
It is rather surprising that this can be done with the set 
of
all rational numbers! Even though it appears that there are many
more rational numbers than positive integers, it is nonetheless possible
to devise a one-to-one correspondence between them. For simplicity,
let's first consider the problem of devising a one-to-one correspondence
between and 
,
the set of positive rationals. (After we have done this, see
if you can use this to devise a one-to-one correspondence between and .)
Since our goal is effectively to count the positive rationals, let's make
a systematic list of all them. Recalling that a positive rational
number can be expressed as a quotient of two positive integers, consider
this listing:
and .
With a little thought, you should be able to see how to get a one-to-one
correspondence between and ,
thus showing that is
countably infinite. Note that it is not necessary to find a formula
for the correspondence; all that is necessary is the certainty that such
a correspondence exists. There are many other instances in mathematics
that are like this--where the point is to show that something has to happen
or that something exists, rather than to actually exhibit a formula.
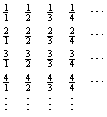
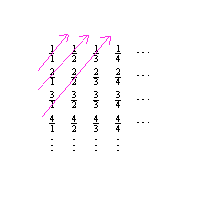
What's Larger than Countably Infinite?
We have just seen that both and are
countably infinite. Is it true that every infinite set is
countably infinite? That is, can every infinite set be put
into one-to-one correspondence with ,
or are some infinite sets "larger" than in
some sense? It turns out that there are indeed different "sizes"
of infinite sets; not all infinite sets are of the same infinite "size"!
An infinite set which cannot be put into one-to-one correspondence with is,
naturally enough, referred to as an uncountable set. A simple
example of an uncountable set is the set of real numbers between 0 and
1, the unit interval 
.
To see that is
uncountable, we will use the technique of proof by contradiction, which
was used in Vignette 2 to show the existence of infinitely many primes.
It is clear that is
infinite, so let's suppose that were
a countably infinite set. (If we show that this leads to a
contradiction, then we will have proven that is
uncountable.) Now the numbers in can
all be expressed in decimal form, beginning with the whole number part
0. (Even the number 1 can be written this way, as 
.)
If the set of such numbers were countable, then we could list them in order
of their correspondence with the positive integers:
.
To obtain the needed contradiction, consider the new number 
,
where we choose each digit bi to be any digit
at least 2 off from aii . This construction assures
that n is different from each of n1, n2,
n3
and so on. This shows that we were really not able to make a countable
list of all of the numbers in after
all! Our conclusion is that is
an uncountable set, representing a new and larger kind of infinite size.
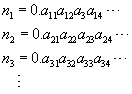
Is There More?
The branch of mathematics that deals with sets and their cardinality is known as set theory. Although Georg Cantor's discovery of the differences among the cardinalities of various infinite sets came as quite a shock to the mathematical community in the 1870's, it is now well understood that there is a whole new type of arithmetic based on the transfinite numbers, the cardinalities of infinite sets.
Further Exploration
