Vignette 1
The Möbius Band and Other Topological Surfaces

In the mathematical field known as topology, one of the main objectives is the classification of surfaces.  That is, we study ways of categorizing and distinguishing among various surfaces.  In this vignette, we will explore several interesting surfaces, which can be thought of as being constructed out of a sheet of paper.  So grab some paper, a pencil, tape and scissors, and follow along!

The Cylinder

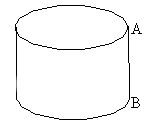
Begin with a rectangle cut from paper.  On two opposite ends, label the vertices A and B, as shown.

Now bring the two ends together so that the A's match up and the B's match up.  You have just created another surface, called a cylinder.  (To make this somewhat more permanent, use some tape.)  Your cylinder should look like this:

In constructing this new surface, we have "identified" the two edges of the original rectangular strip of paper.  That is, mathematically, we regard the points that were originally on the left edge as being identical to the points that were originally on the right edge.  Rather than labeling the corners, we could have specified the identification by using arrows--the idea being that the new surface would be formed by identifying edges so that the directions of the arrows match up.  Here is the cylinder, presented in this way:
The cylinder is regarded as topologically distinct from the original rectangle.  One fundamental difference between those two surfaces--the rectangle and the cylinder--is that if you cut the rectangle from top to bottom, there will be two pieces, whereas if you cut the cylinder from top to bottom, there will be only one piece!

The Möbius Band

Mathematicians are always asking questions about what happens if you modify a technique or change your assumptions.  This is precisely how new mathematics is created.  For example, suppose we change the way in which the edges are identified in the construction above.  This time, cut out a rectangle and identify (by taping) the edges as shown by the arrows in the diagram below:

The resulting surface, known as a Möbius band, should look like this:
The Möbius band is topologically distinct from the rectangle and the cylinder.  Some fundamental differences are that the Möbius band has only one side, whereas the other surfaces have two sides.  To convince yourself of this, take a pencil and start to draw a line around the length of the Möbius band.  You will find that the line will eventually be right behind where you began; and if you continue, you will come back to the starting point.  Another distinction between the Möbius band and the cylinder is that the Möbius band has only one boundary edge, whereas the cylinder has two boundary edges!

The Torus

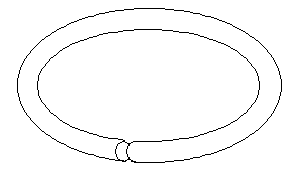
A torus is a surface shaped like a bagel--or an inner tube.  A torus can be constructed--at least in theory--by taking a cylinder (such as a paper towel tube) and joining the ends of the cylinder.  Now if you try this with an actual cardboard or paper cylinder, it will not work so well.  But in the mathematical construction, we think of our surfaces as being stretchable--as though they were made out of rubber.  Here is a cylinder in the process of being bent into a torus:

Since the torus is formed out of a cylinder by identifying the two circular ends, we can describe the torus as a rectangular sheet with edges identified in the following ways:
In this "flattened torus," think of identifying the edges with the double arrows to form a long cylinder, and then identify the circular ends--the sides depicted with the single arrows.

Can you describe some characteristic of the torus that distinguishes it from the other surfaces described above?  (Think in terms of cutting it, or think in terms of boundary edges.)

The Klein Bottle

In the spirit of further mathematical exploration, we might consider the surface that would result from the following identifications:

To form this surface, we first create a cylinder by identifying the edges marked with the double arrows.  Then, instead of identifying the circular edges of the cylinder in the previous way to form a torus, we identify them with a reversal of orientation.  But don't bother trying to construct this surface with paper, because it cannot be done in 3-dimensional space!  This is because the identification of the two ends seems to require that the cylinder pass through itself, which would mean that more points are being identified than just the ends.

However, the surface, which is known as a Klein bottle, can be embedded in 4-dimensional space.  And we can certainly continue to think of the Klein bottle as the "flattened" model above, with the edges identified as shown.  Using a computer, it is possible to draw a "projection" of a Klein bottle in 3-space:

Don't let this talk of 4-dimensional space bother you too much.  The idea of having to use an additional dimension to accomplish the edge identification in the Klein bottle is analogous to the idea of taking a line segment (which is one-dimensional) and identifying the endpoints, to form a circle.  The identification cannot be carried out in the original 1-dimensional space, but is easily done in 2-dimensional space.

Further Exploration
 


Copyright © 2000 by Carl R. Spitznagel