Vignette 8
Symmetries in Geometry

One of the things studied in geometry is the notion of congruence of geometric objects.  The point of view that is usually taken is to ask whether two objects are congruent, and to look for conditions that imply the congruence of objects.  In plane geometry there are a number of theorems of this sort -- known by labels such as SAS, ASA, and so on.

How Many Congruences Are There?

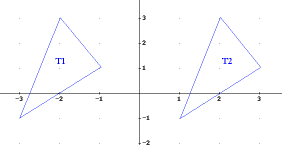
We will define a congruence between two geometric objects to be a rigid motion of the plane that maps one of the objects onto the other.  When two objects are congruent, we can then pose the problem of finding all of the rigid motions of the plane that establish this congruence.  For instance, if the two triangles below are labeled T1 and T2, then it is clear that the rigid motion "shift all points to the right by 4 units" maps T1 onto T2 , and thus is a congruence between T1 and T2 .

But are there any other rigid motions of the plane that also establish the congruence between T1 and T2 ?   For example, could we rotate the plane, reflect it around some line, and/or shift it, to find a different way to make T1 and T2 coincide?  For an arbitrarily shaped triangle, this is a relatively difficult question, so let's start with a more specific triangle, and hopefully the question will be easier to answer.  (This is a favorite trick of mathematicians in the creation of new mathematics -- if you can't answer the question that you have, try making the question easier!)

Rigid Motions of the Equilateral Triangle

Consider an equilateral triangle in the plane.  We will ask what rigid motions of the plane will map the triangle onto itself.  As an aid to understanding what is happening, draw two congruent equilateral triangles on a sheet of paper.  Cut one of the triangles out of the paper.  Label the vertices (on both sides of the paper, in the case of the one you cut out):

Now place your cut-out triangle on top of the other one, so you can begin to explore the rigid motions of the plane that will map the triangle onto itself.  One obvious such rigid motion is rotation counterclockwise by 120o .  Your superimposed triangles should now look like this:
This rigid motion can be identified by the positions of the vertices: the A vertex got mapped to the B location, the B vertex to the C location, and the C vertex to the A location.  We could denote this rigid motion by the notation
Actually, we usually just omit the arrows, and write
You can probably now figure out that another rigid motion of the triangle is , which corresponds to rotation counterclockwise by 240o.  In true mathematical spirit, we now say "OK, what about rotation by 360o?"  This is indeed another rigid motion of the triangle.  In our new notation, it would be .  This rigid motion is actually the identity function, because its net effect is to change nothing.

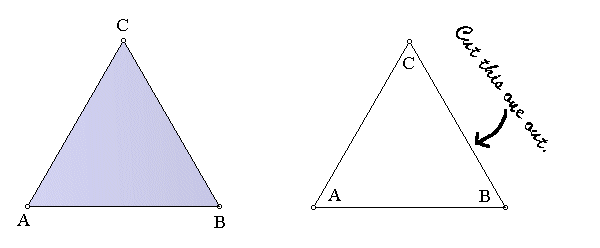
You should be able to convince yourself that these are the only rotations of the plane that map the triangle to itself.  Every  other such rotation is really just one of these three in disguise -- for example, rotation clockwise by 120o is the same transformation as rotation counterclockwise by 240o , and rotation by 480o is the same as rotation by 120o.  So are there any other rigid motions that will map the triangle to itself?

A little reflection (sorry about the pun!) will suggest that if you reflect the triangle around one of the three lines shown in the following picture, this will give another rigid motion of the triangle.

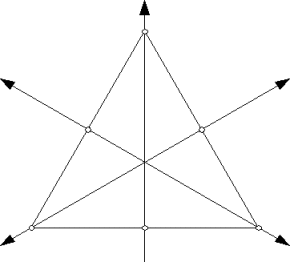
So far, this gives us 6 rigid motions, or "symmetries," of the equilateral triangle.  They are:
 

Rotations Reflections

Before continuing, be sure that you understand how the reflections a, b and c work, and which line of symmetry each is associated with.

Do We Have All of Them?

Have we now identified all of the symmetries (rigid motions) of the equilateral triangle, or might we have overlooked some that are not so obvious?  Here's a way to convince ourselves that we have found all of them.  A rigid motion of the triangle must map a vertex to a vertex, and of course two different vertices cannot map to the same vertex.  So, in effect, a rigid motion permutes -- that is, rearranges -- the listing of vertices.  In the notation for rigid motions that we introduced above, each possible ordering of the vertices in the lower row represents such a permutation.  Since there are only such permutations, and we have already found six of them, then we must have all of them.

The Algebra of Symmetries

Now here is where the fun begins!!  If we perform one rigid motion of the equilateral triangle, and then follow that with another rigid motion, the result should also be a rigid motion.  Given two rigid motions to be performed in succession, we can determine the rigid motion that results in either of two ways -- using the paper triangles, or by doing some algebra.  The neat thing about this is that the algebra thus represents a concept that began in a purely geometric way.

For example, consider the effect of doing reflection b, followed by rotation r2 .  Using your paper triangles, perform reflection b by holding vertex B of the top triangle in its position while you switch the positions of the other two vertices.  Your triangles should then look like this:

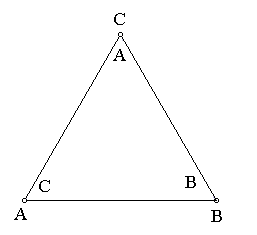
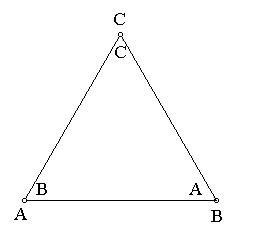
Now perform rotation r2 by holding the center point in place while you rotate counterclockwise by 240o.  (This is equivalent to rotating through two vertex permutations.)  Your triangles should now look like this:
That is, the effect of performing b, followed by r2 , is , which is the rigid motion we have called c.

We can see this algebraically, as well.  To compute the effect of doing reflection b, followed by rotation r2 , we simply compute the composition of these two functions.  Since b is done first, the composition is written as .  Since  and , under the composition vertex A first maps to C (by way of the rigid motion b), and then r2 takes over and maps C to B.  The net effect is that A maps to B.  Similarly, B maps first to B (via b), and then thatB maps to A (via r2 ), for the net effect that B maps to A.  Similarly, we see that under  , , for the net effect that C maps to C.  Thus, , as we also saw geometrically.

The Operation Table for the Symmetries of the Triangle

What we have just seen can be summarized by saying that composition is an operation on the set of rigid motions of the triangle.  This just means that composition is a way of combining two rigid motions to obtain another rigid motion -- in much the same way that addition and multiplication are ways of combining two numbers to obtain another number.  The results of this operation can be summarized in a table, similar to the addition and multiplication tables that you had to memorize in the early grades of school.  The fact that , which we saw above, can be recorded as one of the entries in this table:

See how many of the other table entries you can fill in.  Some important hints: What's Next?

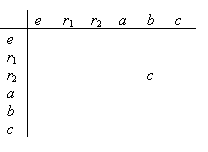
The set of symmetries (rigid motions) of the triangle, along with the operation table described above, is an important example of what is called a group.  In general, a group is a set, along with an operation, satisfying certain properties.  Groups (and the example of the group of rigid motions of the equilateral triangle) are studied in the branch of mathematics known as abstract algebra.  Groups can be formed by looking at symmetries of other geometric objects, such as a square or a regular pentagon.  These groups are often referred to as symmetry groups.

Further Exploration



Copyright © 2000 by Carl R. Spitznagel