The nineteenth century German mathematician Leopold Kronecker is reputed to have said "Die ganzen Zahlen hat Gott gemacht, alles andere ist Menschenwerk" (The whole numbers were made by God, all else is the work of mankind). Indeed, negative integers fill an algebraic void left by the positive integers, by providing solutions to equations such as x + 1 = 0. This leads to the creation of the system of integers, in which all such equations have solutions. The system of rational numbers in turn fills an algebraic void left by the integers, by providing solutions to equations such as 2x - 1 = 0. And in a similar way, the system of real numbers fills an algebraic void left by the rational numbers, by providing solutions to equations such as x2 - 2 = 0.
The System of Complex Numbers
Does the process of creation of new "numbers" end with the real numbers? In spite of creating these successively larger number systems in order to have solutions to more and more equations, there are still equations that have no solution, the simplest being the innocent-looking x2 + 1 = 0. Rather than simply declaring such equations to be unsolvable, why not extend the system of real numbers to include solutions to equations of this type? In order to do this, let us postulate the existence of such a larger system of numbers, which we will call the complex numbers, and agree that in this larger system, a solution to the equation x2 + 1 = 0 will be denoted by the letter i. Must there be any other numbers in such a number system?
Algebraic closure is a property that we would certainly expect
any set that calls itself a number system to have. This means that
adding and multiplying any two such numbers should result in another such
number. In particular, then, since this new number system is an extension
of (that is, a more inclusive set than) the real numbers, our new complex
number system must contain all the real numbers, in addition to at least
the one new number i. Algebraic closure then requires that
our new system contain numbers to represent 2i, 3i, 4.783i,
-8.6i, and even ![]() and
and ![]() .
So we must include at least all real multiples of i. (These
are called the pure imaginary numbers.) But then we must also
include sums of real numbers with the various multiples of i, in
order to retain the desired algebraic closure. That is, we must include
at least the "numbers" of the form
.
So we must include at least all real multiples of i. (These
are called the pure imaginary numbers.) But then we must also
include sums of real numbers with the various multiples of i, in
order to retain the desired algebraic closure. That is, we must include
at least the "numbers" of the form ![]() .
Must any other new numbers be included in our new system of complex numbers?
.
Must any other new numbers be included in our new system of complex numbers?
Addition and Multiplication of Complex Numbers
For the time being, at least, let's try out what we have built so far, and see how it works. If it is fails to have some property that a number system should have, or if it does not permit solving all the equations that we would like to have solutions to, then we can always go back and throw in more new "numbers."
Of course, we expect that a number system will have operations of addition and multiplication defined in such a way that the customary commutative, associative and distributive properties will hold. Because of this, we are essentially forced to define addition of complex numbers so that
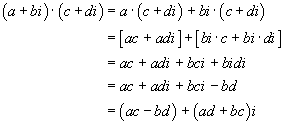
Note that in going from the third line to the fourth line of the equation for multiplication, we have used the fact that i is a solution to the equation x2 + 1 = 0, so that i2 + 1 = 0, and hence i2 = -1. Also notice that complex numbers are added by simply adding the real parts and the imaginary parts, but that multiplication is performed by the slightly more complicated formula shown above.
Although it is somewhat tedious, one can verify that the complex number system, with the addition and multiplication shown above, satisfies the commutative, associative and distributive properties usually expected of a number system. There is also a division operation for complex numbers, which gives a quotient of any two complex numbers (as long as the divisor is not zero).
Solving Equations with Complex Numbers
Remembering that the reason for introducing the complex number system was the fact that equations like x2 + 1 = 0 have no solution in the system of real numbers, we should now look at how much improvement has been made with the introduction of the system of complex numbers. Of course, we now have a solution for x2 + 1 = 0, namely x = i. But what about other equations?
Although we cannot prove it here because the proof uses a fair amount of advanced mathematics, we can at least state the important result known as the Fundamental Theorem of Algebra:
Every polynomial of positive degree with coefficients in the system of complex numbers has a zero in the system of complex numbers. Moreover, every such polynomial can be factored linearly in the system of complex numbers.
This means that the program of expanding number systems in order to be able to solve equations is completed with the complex number system. Not only do all polynomial equations with real numbers as coefficients have solutions, but even if we use complex numbers as coefficients, there will still be solutions. The fact that polynomials can be factored into linear factors means, for instance, that a polynomial equation with degree n will have exactly n roots (counting any repeated roots as separate roots) in the system of complex numbers.
Roots and Graphs
You should be familiar with the relation between the real roots of a
polynomial equation and the x-intercepts of the graph of the polynomial.
For example, the graph of ![]() ,
as shown below, has two x-intercepts:
,
as shown below, has two x-intercepts:
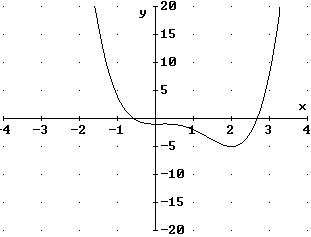
What about the roots of the equation x2 + 1 = 0 ?
According to the Fundamental Theorem of Algebra, there should be exactly
two roots in the system of complex numbers. But neither of these
is a real number, because the graph of y = x2
+ 1 does not cross the x-axis. (Indeed, the fact that this
equation does not have any real roots is what started the whole development
of the complex numbers!) One of the roots, we know, is the complex
number denoted by i. It is easy to see by inspection that
the other root must be the number -i, for ![]() .
Thus, in the system of complex numbers, there are two square roots of -1,
namely i and -i.
.
Thus, in the system of complex numbers, there are two square roots of -1,
namely i and -i.
Can you find the four 4th roots of 1 (that is, the four complex numbers that are roots of the equation x4 - 1 = 0 )?
Finding Roots
The Fundamental Theorem of Algebra is an example of what is known in
mathematics as an existence theorem. It tells us that something
exists or is guaranteed to happen, but it does not tell us how to find
that thing. We know, for instance, that the equation ![]() has
four roots in the complex number system, but the problem of finding those
roots is not necessarily easy!
has
four roots in the complex number system, but the problem of finding those
roots is not necessarily easy!
Every polynomial equation of degree 4 or less can be solved by formulas
-- similar to the quadratic formula, but considerably more involved.
For instance, if you ask the computer algebra system DERIVE to solve the
equation ![]() ,
the solution is so involved that it extends approximately ten screen-widths!
In this case, a numerical approximation is much easier to understand, and
can also be obtained easily from a computer algebra system.
,
the solution is so involved that it extends approximately ten screen-widths!
In this case, a numerical approximation is much easier to understand, and
can also be obtained easily from a computer algebra system.
Further Exploration