Vignette
1
The
Möbius Band and Other Topological Surfaces
In the mathematical field known as topology, one of the main
objectives is the classification of surfaces. That is, we study ways
of categorizing and distinguishing among various surfaces. In this
vignette, we will explore several interesting surfaces, which can be thought
of as being constructed out of a sheet of paper. So grab some paper,
a pencil, tape and scissors, and follow along!
The Cylinder
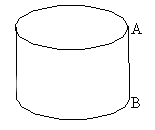
Begin with a rectangle cut from paper. On two opposite ends, label
the vertices A and B, as shown.

Now bring the two ends together so that the A's match up and the B's match
up. You have just created another surface, called a cylinder.
(To make this somewhat more permanent, use some tape.) Your cylinder
should look like this:
In constructing this new surface, we have "identified" the two edges of
the original rectangular strip of paper. That is, mathematically,
we regard the points that were originally on the left edge as being identical
to the points that were originally on the right edge. Rather
than labeling the corners, we could have specified the identification by
using arrows--the idea being that the new surface would be formed by identifying
edges so that the directions of the arrows match up. Here is the
cylinder, presented in this way:
 The cylinder is regarded as topologically distinct from the original rectangle.
One fundamental difference between those two surfaces--the rectangle and
the cylinder--is that if you cut the rectangle from top to bottom, there
will be two pieces, whereas if you cut the cylinder from top to bottom,
there will be only one piece!
The cylinder is regarded as topologically distinct from the original rectangle.
One fundamental difference between those two surfaces--the rectangle and
the cylinder--is that if you cut the rectangle from top to bottom, there
will be two pieces, whereas if you cut the cylinder from top to bottom,
there will be only one piece!
The Möbius Band
Mathematicians are always asking questions about what happens if you
modify a technique or change your assumptions. This is precisely
how new mathematics is created. For example, suppose we change the
way in which the edges are identified in the construction above.
This time, cut out a rectangle and identify (by taping) the edges as shown
by the arrows in the diagram below:
 The resulting surface, known as a Möbius band, should look
like this:
The resulting surface, known as a Möbius band, should look
like this:
 The Möbius band is topologically distinct from the rectangle and the
cylinder. Some fundamental differences are that the Möbius band
has only one side, whereas the other surfaces have two sides. To
convince yourself of this, take a pencil and start to draw a line around
the length of the Möbius band. You will find that the line will
eventually be right behind where you began; and if you continue, you will
come back to the starting point. Another distinction between the
Möbius band and the cylinder is that the Möbius band has only
one boundary edge, whereas the cylinder has two boundary edges!
The Möbius band is topologically distinct from the rectangle and the
cylinder. Some fundamental differences are that the Möbius band
has only one side, whereas the other surfaces have two sides. To
convince yourself of this, take a pencil and start to draw a line around
the length of the Möbius band. You will find that the line will
eventually be right behind where you began; and if you continue, you will
come back to the starting point. Another distinction between the
Möbius band and the cylinder is that the Möbius band has only
one boundary edge, whereas the cylinder has two boundary edges!
The Torus
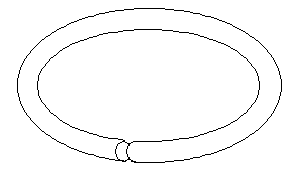
A torus is a surface shaped like a bagel--or an inner tube.
A torus can be constructed--at least in theory--by taking a cylinder (such
as a paper towel tube) and joining the ends of the cylinder. Now
if you try this with an actual cardboard or paper cylinder, it will not
work so well. But in the mathematical construction, we think of our
surfaces as being stretchable--as though they were made out of rubber.
Here is a cylinder in the process of being bent into a torus:
Since the torus is formed out of a cylinder by identifying the two circular
ends, we can describe the torus as a rectangular sheet with edges identified
in the following ways:
 In this "flattened torus," think of identifying the edges with the double
arrows to form a long cylinder, and then identify the circular ends--the
sides depicted with the single arrows.
In this "flattened torus," think of identifying the edges with the double
arrows to form a long cylinder, and then identify the circular ends--the
sides depicted with the single arrows.
Can you describe some characteristic of the torus that distinguishes
it from the other surfaces described above? (Think in terms of cutting
it, or think in terms of boundary edges.)
The Klein Bottle
In the spirit of further mathematical exploration, we might consider
the surface that would result from the following identifications:
 To form this surface, we first create a cylinder by identifying the edges
marked with the double arrows. Then, instead of identifying the circular
edges of the cylinder in the previous way to form a torus, we identify
them with a reversal of orientation. But don't bother trying to construct
this surface with paper, because it cannot be done in 3-dimensional space!
This is because the identification of the two ends seems to require that
the cylinder pass through itself, which would mean that more points are
being identified than just the ends.
To form this surface, we first create a cylinder by identifying the edges
marked with the double arrows. Then, instead of identifying the circular
edges of the cylinder in the previous way to form a torus, we identify
them with a reversal of orientation. But don't bother trying to construct
this surface with paper, because it cannot be done in 3-dimensional space!
This is because the identification of the two ends seems to require that
the cylinder pass through itself, which would mean that more points are
being identified than just the ends.
However, the surface, which is known as a Klein bottle, can be
embedded in 4-dimensional space. And we can certainly continue to
think of the Klein bottle as the "flattened" model above, with the edges
identified as shown. Using a computer, it is possible to draw a "projection"
of a Klein bottle in 3-space:
 Don't let this talk of 4-dimensional space bother you too much. The
idea of having to use an additional dimension to accomplish the edge identification
in the Klein bottle is analogous to the idea of taking a line segment (which
is one-dimensional) and identifying the endpoints, to form a circle.
The identification cannot be carried out in the original 1-dimensional
space, but is easily done in 2-dimensional space.
Don't let this talk of 4-dimensional space bother you too much. The
idea of having to use an additional dimension to accomplish the edge identification
in the Klein bottle is analogous to the idea of taking a line segment (which
is one-dimensional) and identifying the endpoints, to form a circle.
The identification cannot be carried out in the original 1-dimensional
space, but is easily done in 2-dimensional space.
Further Exploration
-
Play Tic-Tac-Toe
on a torus or Klein bottle
-
Instructions for
knitting a Möbius band scarf and a Klein bottle hat
-
Clifford A. Pickover, The Mobius Strip: Dr. August Mobius's Marvelous Band in
Mathematics, Games, Literature, Art, Technology, and Cosmology (Thunder's
Mouth Press, 2006)
-
Ivars Peterson, The Mathematical Tourist: Snapshots of Modern Mathematics.
In JCU Library, call number QA93.P475
-
Stephen Barr, Experiments in Topology. In JCU Library, call
number QA611.B26

Copyright © 2000 by Carl R. Spitznagel









