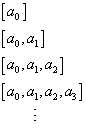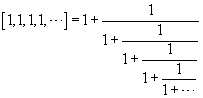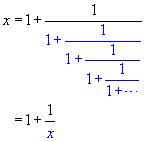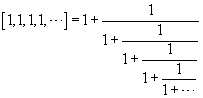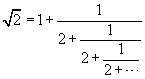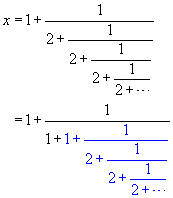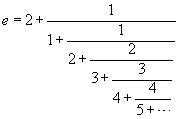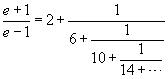Vignette 18
Continued
Fractions
A continued fraction is a fractional expression of the form
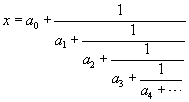 where a0, a1, a2,
a3,
... are integers, all positive, with the possible exception of a0.
As a convenient shorthand notation, we will denote the continued fraction
above by
where a0, a1, a2,
a3,
... are integers, all positive, with the possible exception of a0.
As a convenient shorthand notation, we will denote the continued fraction
above by 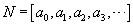 .
.
Finite Continued Fractions
A finite continued fraction -- an expression like that above
that actually ends -- represents a rational number. As an
example,
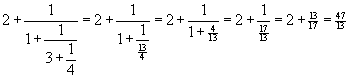
What is perhaps more surprising, every rational number can be represented
as a finite continued fraction! To express a given rational number
as a continued fraction, we need only perform ordinary division.
For example, to express 221/41 as a continued fraction, we divide 221 by
41 to obtain the quotient 5 and remainder16.
That is, 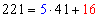 .
We continue the division process, each time dividing the most recent divisor
by the most recent remainder, stopping only when the remainder is 0:
.
We continue the division process, each time dividing the most recent divisor
by the most recent remainder, stopping only when the remainder is 0:
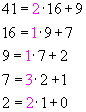
This leads to the continued fraction
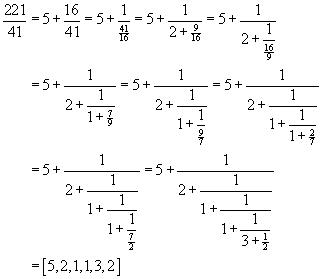
Notice that the numbers 2, 1, 1, 3 and 2 are precisely those colored
magenta
in the repeated divisions above.
Try this process yourself, with the fraction 23/16.
Infinite Continued Fractions
Infinite continued fractions involve more than ordinary arithmetic,
because the chain of fractions never ends. A formal meaning
can be given to an infinite continued fraction in the following way.
The value of the infinite continued fraction 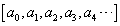 is the limit of the sequence of values of the finite continued fractions
is the limit of the sequence of values of the finite continued fractions
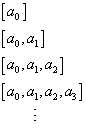 each of which makes sense because it is finite. A somewhat technical
argument shows that every infinite continued fraction represents an irrational
number. Moreover, every irrational number can be expressed as an
infinite continued fraction! This fact was proven by the prolific
Swiss mathematician Leonhard Euler (1707-1783). Euler also derived
many interesting continued fraction formulas, some of which we will see
below.
each of which makes sense because it is finite. A somewhat technical
argument shows that every infinite continued fraction represents an irrational
number. Moreover, every irrational number can be expressed as an
infinite continued fraction! This fact was proven by the prolific
Swiss mathematician Leonhard Euler (1707-1783). Euler also derived
many interesting continued fraction formulas, some of which we will see
below.
The Golden Ratio
The most basic of all continued fractions is the one using all 1's:
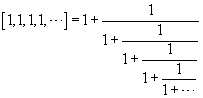 and so a natural question concerns what the value of this continued fraction
is. If we let x denote this value, then
and so a natural question concerns what the value of this continued fraction
is. If we let x denote this value, then
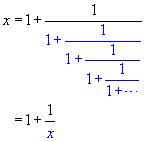 In the equation above, notice that the part colored blue is, in fact, identical
to x, giving the result that
In the equation above, notice that the part colored blue is, in fact, identical
to x, giving the result that 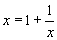 . (Remember that the chain of fractions continues indefinitely, so
that the full expression for x is actually embedded within the expression
for x !) Multiplying the equation
. (Remember that the chain of fractions continues indefinitely, so
that the full expression for x is actually embedded within the expression
for x !) Multiplying the equation 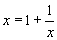 on both sides by x gives us x2 = x + 1
or, equivalently,
on both sides by x gives us x2 = x + 1
or, equivalently, 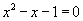 .
Thus, the value of the continued fraction
.
Thus, the value of the continued fraction
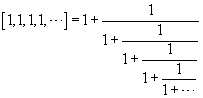 must be a solution to the equation
must be a solution to the equation 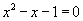 .
Since the value is positive (all of the numbers being added are positive),
the quadratic formula gives us
.
Since the value is positive (all of the numbers being added are positive),
the quadratic formula gives us 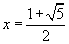 ,
the number known as the golden ratio or golden mean.
This number pops up over and over in unexpected places in mathematics.
The ancient Greeks discovered it in certain geometric constructions, and
used it extensively in their architecture. It occurs repeatedly in
nature, as a limiting value of sequences of ratios in certain measurements
of flowers and other plant life. Psychological tests have indicated
that the most aesthetically pleasing size for a rectangle is one for which
the ratio of length to width is the golden ratio. The golden ratio
appears in art throughout the ages, from Leonardo da Vinci to Piet Mondrian.
So it is certainly fitting that this same number should arise when considering
the most basic of continued fractions!
,
the number known as the golden ratio or golden mean.
This number pops up over and over in unexpected places in mathematics.
The ancient Greeks discovered it in certain geometric constructions, and
used it extensively in their architecture. It occurs repeatedly in
nature, as a limiting value of sequences of ratios in certain measurements
of flowers and other plant life. Psychological tests have indicated
that the most aesthetically pleasing size for a rectangle is one for which
the ratio of length to width is the golden ratio. The golden ratio
appears in art throughout the ages, from Leonardo da Vinci to Piet Mondrian.
So it is certainly fitting that this same number should arise when considering
the most basic of continued fractions!
Some Other Continued Fractions
Euler found that
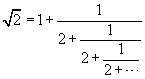 This is actually easy to see, for if we let x denote the value of
this continued fraction, then we have
This is actually easy to see, for if we let x denote the value of
this continued fraction, then we have
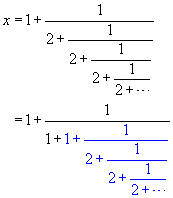
Noticing that the blue part is identical to x, we see that 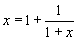 .
It is then easy to solve this equation to see that
.
It is then easy to solve this equation to see that 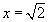 .
(Try this yourself.)
.
(Try this yourself.)
Euler also discovered how to write an infinite series as a continued
fraction, and vice versa. Using this technique, he found a number
of interesting continued fractions involving the number e -- the
number used as the base of the natural logarithm function. Among
the formulas that he discovered are:
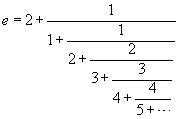 and
and
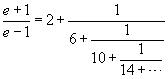
Further Exploration

Copyright © 2000 by Carl R. Spitznagel
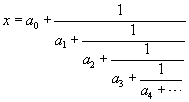
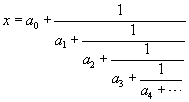
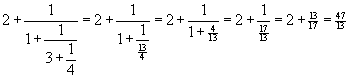
![]() .
We continue the division process, each time dividing the most recent divisor
by the most recent remainder, stopping only when the remainder is 0:
.
We continue the division process, each time dividing the most recent divisor
by the most recent remainder, stopping only when the remainder is 0:
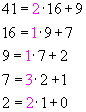
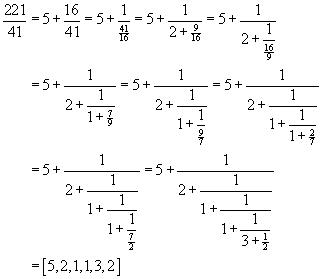
![]() is the limit of the sequence of values of the finite continued fractions
is the limit of the sequence of values of the finite continued fractions